Analisis Penjadwalan Metode Diagram Preseden ( PDM )
Pada Pembahasan
Jaringan Kerja sebelumnya, telah disinggung bahwa di samping bentuk AOA juga dikenal AON atau kegiatan berada di
Node ( activity on node ). Metode preseden diagram (PDM) adalah jaringan kerja yang termasuk klasifikasi AON.
Di sini kegiatan dituliskan di dalam node yang umumnya berbentuk segi empat, sedangkan anak panah hanya sebagai petunjuk hubungan antara kegiatan- kegiatan yang bersangkutan.
Dengan demikian,
Dummy yang dalam CPM dan PERT merupakan tanda yang penting untuk menunjukkan hubungan ketergantungan, di dalam PDM tidak diperlukan. Di pembahasan ini akan disajikan
Dasar-dasar menyusun PDM beserta konstrain yang dapat terjadi antara kegiatan-kegiatan,
Cara menghitung jalur kritis serta contoh perhitungan, dengan memasukkan unsur kemungkinan adanya splitting dalam melaksanakan kegiatan.
Kegiatan Tumpang Tindih
Aturan dasar CPM atau AOA mengatakan bahwa suatu kegiatan boleh dimulai setelah pekerjaan terdahulu (predecessor) selesai, maka untuk proyek dengan rangkaian kegiatan yang tumpang tindih (overlaping) dan berulang-ulang akan memerlukan garis dummy yang banyak sekali, sehingga tidak praktis dan kompleks.
Sebagai contoh, Gambar dibawah ini memperlihatkan Jaringan Kerja AOA proyek memasang pipa, yang terdiri dari kegiatankegiatan menggali tanah, meletakkan pipa dan menimbun kembali.
 |
| Proyek memasang Pipa |
Misalkan setelah diteliti untuk mempersingkat waktu, komponen kegiatan proyek dilaksanakan secara tumpang tindih, yaitu pekerjaan meletakkan pipa dimulai setelah pekerjaan menggali tanah selesai 40 persen dari panjang keseluruhan, jadi tidak perlu menunggu selesai 100 persen.
Demikian halnya pekerjaan berikutnya. Untuk maksud tersebut, bila dipakai Metode CPM, kegiatan harus dikelompokkan menjadi beberapa bagian, yang dalam contoh di atas ditunjukkan dengan angka-angka bagian 40persen dan 60 persen.
Terlihat bahwa jaringan kerja yang dihasilkan Gambar dibawah ini menjadi kompleks dan memerlukan banyak dummy.
 |
| Kegiatan-kegiatan dipecah |
Bila proyek tersebut disajikan dengan metode PDM, maka akan terlihat seperti gambar dibawah ini, akan menghasilkan diagram yang relatif sederhana. Oleh karena itu, metode ini banyak dijumpai pada proyek-proyek engineering-konstruksi yang kaya akan pekerjaan tumpang tindih dan pengulangan, seperti pemasangan pipa, pembangunan gedung bertingkat, pengaspalan, dan lain-lain.
 |
| Kegiatan dalam Metode PDM |
Kegiatan, Peristiwa dan Atribut.
Kegiatan dan
peristiwa pada PDM ditulis dalam node yang berbentuk kotak segiempat. Definisi kegiatan dan peristiwa sama seperti pada CPM. Hanya perlu ditekankan di sini bahwa
dalam PDM kotak tersebut menandai suatu kegiatan, dengan demikian harus dicantumkan
identitas kegiatan dan kurun waktunya. Adapun peristiwa merupakan ujung ujung kegiatan. Setiap node mempunyai dua peristiwa yaitu peristiwa awal dan akhir.
Ruangan dalam node dibagi menjadi kompartemen-kompartemen kecil yang berisi keterangan spesifik dari kegiatan dan peristiwa yang bersangkutan dan dinamakan a tribut.
Pengaturan denah (layout) kompartemen dan macam serta jumlah atribut yang hendak dicantumkan bervariasi sesuai keperluan dan keinginan pemakai. Beberapa atribut yang sering dicantumkan di antaranya adalah kurun waktu kegiatan (D), identitas kegiata (nomor dan nama), mulai dan selesainya kegiatan (ES, LS, EF, LF, dan lain-lain).
Kadang-kadang di dalam kotak node dibuat kolom kecil sebagai tempat mencantumkan tanda persen (%) penyelesaian pekerjaan. Kolom ini akan membantu mempermudah mengamati dan memonitor progres pelaksanaan kegiatan.
 |
| Denah yang Lazim pada Node |
Konstrain dan Lag
Telah disinggung di sebelumnya bahwa pada PDM, anak panah hanya sebagai penghubung atau memberikan keterangan hubungan antarkegiatan, dan bukan menyatakan kurun waktu kegiatan seperti halnya pada CPM.
Tetapi karena PDM tidak terbatas pada aturan dasar jaringan kerja CPM (kegiatan boleh mulai setelah kegiatan yang mendahuluinya selesai), maka hubungan antarkegiatan berkembang menjadi beberapa kemungkinan berupa konstrain.
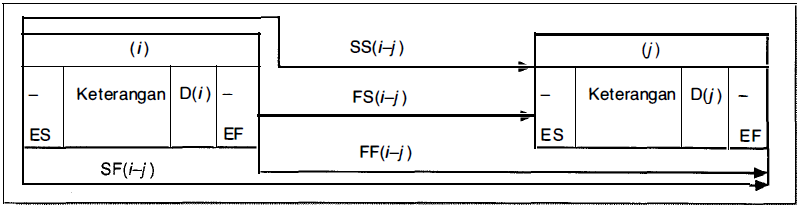
Konstrain menunjukkan hubungan antar kegiatan dengan satu garis dari node terdahulu ke node berikutnya. Satu konstrain hanya dapat menghubungkan dua node. Karena setiap node memiliki dua ujung, yaitu ujung awal atau mulai = (S) dan ujung akhir atau selesai = ( F) , maka ada 4 macam konstrain, yaitu awal ke awal (SS), awal ke akhir (SF), akhir ke akhir (FF) dan akhir ke awal (FS).
Pada garis konstrain dibubuhkan penjelasan mengenai waktu mendahului (lead) atau terlambat tertunda (Jag). Bila kegiatan (i) mendahului (j) dan satuan waktu adalah hari, maka penjelasan lebih lanjut adalah sebagai berikut:
Konstrain Selesai ke Mulai - FS
Konstrain ini memberikan penjelasan hubungan antara mulainya suatu kegiatan dengan selesainya kegiatan terdahulu. Dirumuskan sebagai FS(i-j) = a yang berarti kegiatan (j) mulai a hari, setelah kegiatan yang mendahuluinya (i) selesai.
Proyek selalu menginginkan besar angka a sama dengan 0 kecuali bila dijumpai hal-hal tertentu, misalnya :
- Akibat iklim yang tak dapat dicegah.
- Proses kimia atau fisika seperti waktu pengeringan adukan semen.
- Mengurus perijinan.
Jenis konstrain ini identik dengan kaidah utama jaringan kerja-CPM atau PERT, yaitu suatu kegiatan dapat mulai bila kegiatan yang mendahuluinya (predecessor) telah selesai.
Konstrain Mulai ke Mulai - SS
Memberikan penjelasan hubungan antara mulainya suatu kegiatan dengan mulainya kegiatan terdahulu. Atau SS (i-j) = b yang berarti suatu kegiatan (j) mulai setelah b hari kegiatan terdahulu (i) mulai.
Konstrain semacam ini terjadi bila sebelum kegiatan terdahulu selesai 100 persen, maka kegiatan (j) boleh mulai. Atau kegiatan (j) boleh mulai setelah bagian tertentu dari kegiatan (i) selesai.
Besar angka b tidak boleh melebihi angka kurun waktu kegiatan terdahulu, karena per definisi b adalah sebagian dari kurun waktu kegiatan terdahulu. Jadi, di sini terjadi kegiatan tumpang tindih.
Konstrain Selesai ke Selesai - FF
Memberikan penjelasan hubungan antara selesainya suatu kegiatan dengan selesainya kegiatan terdahulu. Atau FF (i-j) = c yang berarti suatu kegiatan (j) selesai setelah c hari kegiatan terdahulu (i) selesai.
Konstrain semacam ini mencegah selesainya suatu kegiatan mencapai 100%, sebelum kegiatan yang terdahulu telah sekian (= c) hari selesai. Besar angka c tidak boleh melebihi angka kurun waktu kegiatan yang bersangkutan (j).
Dari Gambar diatas ( kegiatan yang di sajikan dengan Metode PDM ) sebagai contoh terlihat bahwa kegiatan (j) boleh mulai sembarang waktu, tetapi pada waktu kegiatan (i) selesai, harus masih ada porsi kegiatan (j) yang belum selesai. Jadi, misalkan selesainya kegiatan (i) terlambat, maka selesainya kegiatan (j) ikut terlambat.
Konstrain Mulai ke Selesai - SF
Menjelaskan hubungan antara selesainya kegiatan dengan mulainya kegiatan terdahulu. Dituliskan dengan SF (i-j)= d, yang berarti suatu kegiatan (j) selesai setelah d hari kegiatan (i) terdahulu mulai. Jadi, dalam hal ini sebagian dari porsi kegiatan terdahulu harus selesai sebelum bagian akhir kegiatan yang dimaksud boleh diselesaikan.
Tanda Konstrain dalam Jaringan Kerja
Gambar dibawah ini memperlihatkan penulisan konstrain pada PDM, yaitu dicantumkan di atas anak panah yang menghubungkan dua kegiatan.
 |
| Konstrain pada PDM |
Kadang-kadang dijumpai satu kegiatan memiliki hubungan konstrain dengan lebih dari satu kegiatan seperti ditunjukkan oleh Gambar dibawah ini atau suatu multikonstrain, yaitu dua kegiatan dihubungkan oleh lebih dari satu konstrain seperti pada Gambar dibawahnya.
 |
| Kegiatan yang mempunyai hubungan konstrain a |
 |
| Multi Konstrin antara kegiatan |
Jadi, dalam menyusun jaringan PDM, khususnya menentukan urutan ketergantungan, mengingat adanya bermacam konstrain di atas, maka lebih banyak faktor harus diperhatikan dibanding CPM. Faktor ini dapat dikaji misalkan dengan menjawab berbagai pertanyaan seperti berikut :
- Kegiatan mana boleh mulai, sesudah kegiatan tertentu A selesai, berapa lama jarak waktu antara selesainya kegiatan A dengan mulainya kegiatan berikutnya.
- Sebelum kegiatan tertentu B boleh mulai, dan berapa lama tenggang waktunya.
- Kegiatan mana harus mulai sesudah kegiatan tertentu C mulai dan berapa lama jarak waktunya.
Pertanyaan-pertanyaan di atas merupakan bagian dari serentetan faktor-faktor yang perlu dianalisis sebelum mulai menyusun jaringan PDM.
Menyusun jaringan PDM
Setelah membahas terminologi, atribut, dan parameter yang berkaitan dengan PDM maka Gambar dibawah ini adalah contoh PDM suatu proyek terdiri dari tiga kegiatan lengkap dengan atribut dan parameter yang bersangkutan, yang semula disajikan dalam bentuk AOA.
 |
| Kegiatan dikerjakan berurutan, penyelesaian proyek total = 22 hari |
Sedangkan potensi penghematan waktu, dijelaskan dengan metode bagan balok berskala waktu yaitu pada Gambar dibawah ini.
 |
| Kegiatan tumpang tindih, penyelesaian proyek total = 17 hari |
Bila kegiatan di atas dikerjakan tumpang tindih, hasilnya akan mempersingkat waktu. Misalnya, seperti Gambar diatas yang disajikan dengan bagan balok, terlihat bahwa penyelesaian proyek total berkurang menjadi 17 hari. Hal ini disebabkan adanya tumpang tindih antara kegiatan Mt dengan Mp dan Mp dengan Mk, yaitu setelah Mt berjalan selama 4 hari maka kegiatan Mp mulai.
Demikian halnya dengan Mk terhadap Mp, yaitu setelah Mp berjalan 6 hari, mulailah kegiatan Mk. Jadi mulainya kegiatan yang satu tidak menunggu kegiatan yang lain selesai 100%. Bila Gambar diatas disajikan dengan PDM/ AON akan terlihat seperti Gambar dibawah ini. Penyelesaian proyek total = 17 hari.
 |
| Kegiatan Disusun menjadi PDM/AON |
Identifikasi Jalur Kritis
Dengan adanya parameter yang bertambah banyak, perhitungan untuk mengidentifikasi kegiatan dan jalur kritis akan lebih kompleks karena semakin banyak faktor yang perlu diperhatikan.
Untuk maksud tersebut, dikerjakan analisis serupa dengan metode AOA/ CPM, dengan memperhatikan konstrain yang terkait, seperti terlihat pada Gambar dibawah ini.
 |
| Menghitung ES dan EF |
Hitungan Maju
Berlaku d an ditujukan untuk hal-hal sebagai berikut :
- Menghasilkan ES, EF dan kurun waktu penyelesaian proyek.
- Diambil angka ES terbesar bila lebih satu kegiatan bergabung.
- Notasi (i) bagi kegiatan terdahulu (predecessor) dan (j) kegiatan yang sedang ditinjau.
- Waktu awal dianggap nol.
1. Waktu mulai paling awal dari kegiatan yang sedang ditinjau ES(j), adalah sama dengan angka terbesar dari jumlah angka kegiatan terdahulu ES(i) atau EF(i) ditambah konstrain yang bersangkutan. Karena terdapat empat konstrain, maka bila ditulis dengan rumus menjadi :
 |
| Rumus ES |
2. Angka waktu selesai paling awal kegiatan yang sedang ditinjau EF(j), adalah sama dengan angka waktu mulai paling awal kegiatan tersebut ES(j), ditambah kurun waktu kegiatan yang bersangkutan D(j). Atau ditulis dengan rumus, menjadi :
EF(J) = ES(J) + D(J)
Hitungan Mundur
Berlaku dan ditujukan untuk hal-hal sebagai berikut :
- Menentukan LS, LF dan kurun waktu float.
- Bila lebih dari satu kegiatan bergabung diambil angka LS terkecil.
- Notasi (i) bagi kegiatan yang sedangditinjau sedangkan lj) adalah kegiatan berikutnya.
1 . Hitung LF (i), waktu selesai paling akhir kegiatan (i) yang sedang ditinjau, yang merupakan angka terkecil dari jumlah kegiatan LS dan LF plus konstrain yang bersangkutan.
 |
| Rumus LF |
2. Waktu mulai paling akhir kegiatan yang sedang ditinjau LS(i), adalah sama dengan waktu selesai paling akhir kegiatan tersebut LF(i), dikurangi kurun waktu yang bersangkutan. Atau
LS(i) = LF(i) - D(i)
 |
| Menghitung LS dan LF |
Jalur dan Kegiatan Kritis
Jalur dan kegiatan kritis PDM mempunyai sifat sama seperti CPM/ AOA, yaitu :
- Waktu mulai paling awal dan akhir harus sama .................. ES = LS
- Waktu selesai paling awal dan akhir harus sama .................. EF = LF
- Kurun waktu kegiatan adalah sama dengan perbedaan waktu selesai paling akhir dengan waktu mulai paling awal....................... LF - ES = D
- Bila hanya sebagian dari kegiatan bersifat kritis, maka kegiatan tersebut secara utuh dianggap kritis.
Demikianlah Materi tentang Analisis Metode Diagram Preseden ( PDM ) semoga bermanfaat. Bagi anda yang menyukai Materi ini, bisa mengikuti Materi berikutnya tentang Contoh Menghitung dan Menyusun Jaringan PDM. Segera Ikuti Updetannya melalui facebook.

































.png)


















.png)







